посетителей - 3

Примеры
Здесь приведены примеры задач, которые были решены с помощью описываемой программы. Собственно, на этих (и многих других) задачах и производилась отладка программы. Многие блоки и алгоритмы были написаны как раз в связи с тем, что они понадобились для решения какой-то конкретной задачи.
Структура программы состоит из нескольких этапов и подпрограмм. Это позволяет добавлять новые блоки и изменять уже существующие в соответствии с появляющимися потребностями. Во многом это касается этапа синтаксического разбора входных данных, о котором пока ничего не было сказано.
Синтаксический разбор предложений условий задачи и вопроса происходит в виде вложенных независимых алгоритмов, которые только обмениваются друг с другом входными и выходными данными.
Сначала выделяется текст, заключенный между двумя скобками (или от начала предложения до первой встреченной скобки, а также от последней скобки до конца предложения). На этом уровне также определяется соответствие между правыми и левыми скобками. Далее полученный текст анализируется на наличие и расположение логических связок "И", "ИЛИ", "НЕ", а также выделяется текст, заключенный между ними. На следующем уровне анализируется текст на наличие арифметических знаков, связывающих правую и левую часть отношения: "равно", "больше", "меньше" и т.п., и производится разбивка на левую и правую часть уравнения или неравенства.
Ну и так далее по нисходящей происходит анализ каждого полученного на предыдущем уровне текста. На последнем этапе анализируется свойство: если его еще не существует в дереве свойств, то оно добавляется.
Программа разбора написана без учета имеющихся и известных алгоритмов синтаксического разбора логических предложений (например, разбор предложений, написанных на SQL). Возможно, существует оптимальный и более эффективный алгоритм для решения этой задачи (синтаксического разбора предложения), применение которого позволит ускорить в этой программе процесс расчета и нахождение ответа.
В настоящее время описанный алгоритм реализован на "JavaScript" (для браузера "Internet Explorer") и "PHP" и размещен на сайте http://hsv.dtn.ru. Приведенные ниже задачи (и многие другие) были тестовыми для этого сайта.
Задача 1.
Эта задача представляет собой закон транзитивности и предложена здесь лишь для демонстрации способа формирования входных условий для программы.
Условие задачи:
Из A следует B, из B следует C.
Вопрос:
Истинно ли высказывание "из A следует C"?
Формирование входных данных:
Импликация "из A следует B" равносильна записи "НЕ А ИЛИ В". Таким образом, условие задачи преобразуется в запись: "(НЕ А ИЛИ В) И (НЕ В ИЛИ С)", или "НЕ А И НЕ В ИЛИ НЕ А И С ИЛИ В И НЕ В ИЛИ В И C"
Запись D:
[А В, не_А С, В не_В, В С]
Запись N:
[А не_В, В не_С]
Формирование вопроса:
Определить истинность формулы "НЕ А ИЛИ С". Для этой формулы запись D: "[не_А, С]", запись N: "[А не_С]".
Ответ:
[не_А, С] – "да" (не пусто).
[А не_С] – "нет" (пусто).
Т. е. формула "НЕ А ИЛИ С" истинна.
Задача 2.
Условие задачи:
X,Y,Z – целые неотрицательные числа, и X<Y,Y<Z,Z=4.
Вопрос:
Какие значения принимает X?
Формирование входных данных:
Так как X,Y,Z – целые неотрицательные числа, то в качестве их значений используется размер множества, задающегося свойством – именем переменной.
([X]<[Y] И [Y]<[Z] И [Z]=4 И [X Y,X Z,Y Z]=0).
Формирование вопроса:
[X]
Ответ:
Kmin=0 и Kmax=2, т. е. X может принимать значения от 0 до 2.
Задача 3.
Условие задачи:
Четверо мальчиков со своими отцами катались на колесе обозрения по два человека: взрослый и мальчик. Ни один мальчик не катался со своим отцом. Алексей Иванович катался с Леней. Андрей катался с отцом Коли. Тима катался с отцом Андрея. Федор Степанович катался с сыном Виктора Павловича. Виктор Павлович катался с сыном Алексея Ивановича.
Вопрос:
С кем катался Григорий Александрович, а также и другие взрослые? И как зовут отца каждого мальчика?
Формирование входных данных:
Составить входные данные для задачи не намного легче, чем ее решить. Главное, определить структуру переменных. В данной задаче условия были сформированы следующим образом:
( 1=[имя![АИ] кат] И 1=[имя[АИ] сын] И 1=[имя[ФС] кат] И 1=[имя[ФС] сын] И 1=[имя[ВП] кат] И 1=[имя[ВП] сын] И 1=[имя[ГА] кат] И 1=[имя[ГА] сын] И 1=[дети![Андрей] кат] И 1=[дети[Андрей] сын] И 1=[дети[Тима] кат] И 1=[дети[Тима] сын] И 1=[дети[Коля] кат] И 1=[дети[Коля] сын] И 1=[дети[Леня] кат] И 1=[дети[Леня] сын] И #имя(1=[дети[Андрей] кат #имя] И 1=[дети[Коля] сын #имя]) И #имя(1=[дети[Тима] кат #имя] И 1=[дети[Андрей] сын #имя] ) И #дети(1=[#дети кат имя[ФС]] И 1=[#дети сын имя[ВП]]) И #дети(1=[#дети кат имя[ВП]] И 1=[#дети сын имя[АИ]]) И 0=[не_имя, не_дети, кат сын, не_кат не_сын, имя[АИ] кат дети[не_Леня], имя[не_АИ] кат дети[Леня]])
Ответ:
Ответ к этой задаче представлен в комбинированной форме. Сначала задается вопрос-множество, а потом с учетом ответа строится таблица.
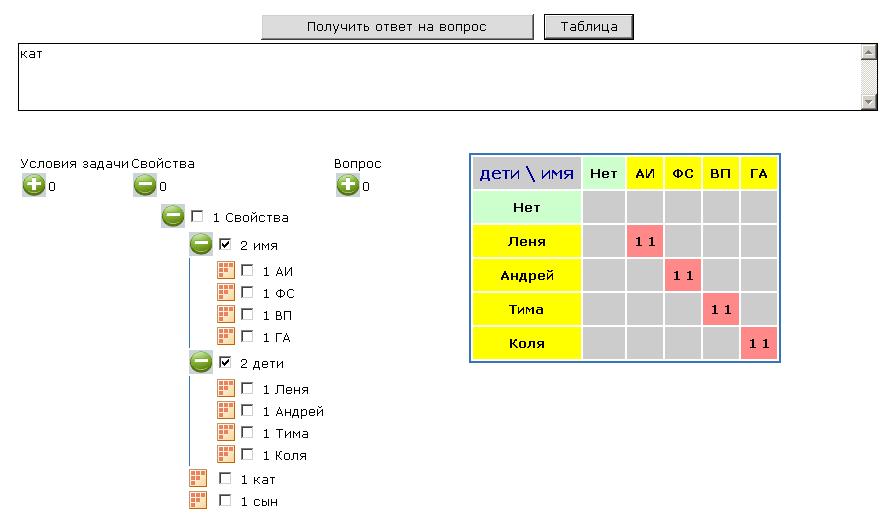
Рисунок 1. К задаче 3. Кто с кем катался
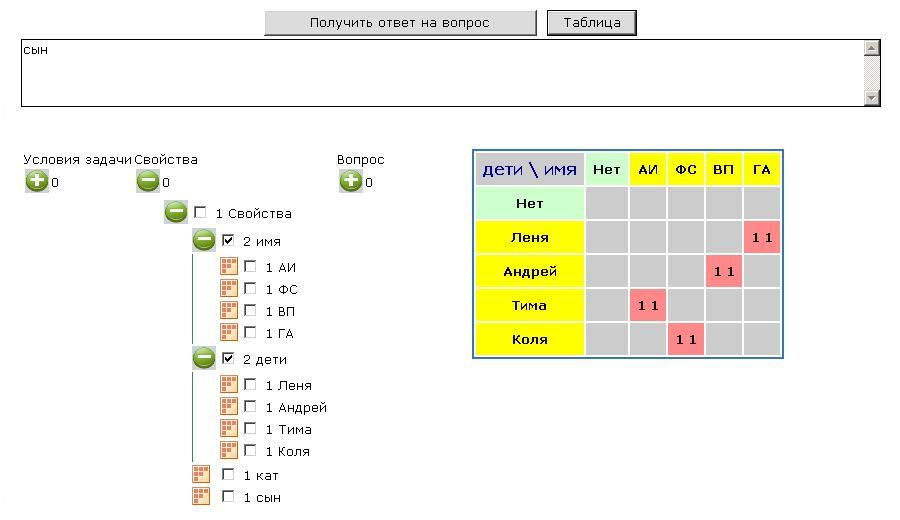
Рисунок 2. К задаче 3. Кто чей отец
Если просто запросить ответ на вопрос "[сын]", то ответом будет – "множество имеет размер 4, т.е. не пусто" (Рисунок 3). Это следует напрямую из условий задачи: заданы 4 объекта, обладающие свойством "сын". Поэтому полезной будет информация, полученная в табличной форме.

Рисунок 3. К задаче 3. Ответ на вопрос
Задача 4.
Условие задачи:
Эта задача известна как задача Эйнштейна. Вот ее условие:
Есть 5 домов каждый разного цвета. В каждом доме живет по одному человеку отличной друг от друга национальности. Каждый жилец пьет только один определенный напиток, курит определенную марку сигарет и держит определенное животное. Никто из 5 человек не пьет одинаковые с другими напитки, не курит одинаковые сигареты и не держит одинаковое животное.\newline
Кроме того:
Англичанин живет в красном доме, датчанин пьет чай, в желтом доме курят "Dunhill", норвежец живет в первом доме, немец курит "Marlboro", в среднем доме пьют молоко, курильщик "PallMall" держит птицу, швед держит собаку, в синем доме держат лошадь, курильщик "PhilipMoris" пьет пиво, в зеленом доме пьют кофе, зеленый дом находится слева от белого, курильщик "Rothmans" живет рядом с тем, кто держит кошку, норвежец живет около голубого дома, курильщик "Rothmans" живет рядом с тем, кто пьет воду.
Вопрос:
Кто держит рыбок?
Формирование входных данных:
Условия задачи сформулированы следующим образом:
[номер[первый]]=1 И [номер[второй]]=1 И [номер[третий]]=1 И [номер[четвертый]]=1 И [номер[пятый]]=1 И 1=[национальность[англичанин] цвет![красный]] И 1=[национальность[датчанин] напиток![чай]] И 1=[цвет[желтый] курит![Dunhill]] И 1=[национальность![норвежец] номер![первый]] И 1=[национальность[немец] курит[Marlboro]] И 1=[номер[третий] напиток![молоко]] И 1=[курит[PallMall] животные![птицы]] И 1=[национальность[швед] животные[собаки]] И 1=[животные[лошади] цвет[синий]] И 1=[курит[PhilipMoris] напиток[пиво]] И 1=[цвет[зеленый] напиток[кофе]] И 1=[животные[рыбы]] И 0=[не_животные, не_напиток, не_курит, не_цвет, не_номер, не_национальность] И *животные([*животные]=1) И *напиток([*напиток]=1) И *курит([*курит]=1) И *цвет([*цвет]=1) И *национальность([*национальность]=1) И ^номер[цвет[зеленый]]+1=^номер[цвет[белый]] И (^номер[курит[Rothmans]]+1=^номер[животные![кошки]] ИЛИ ^номер[курит[Rothmans]]-1=^номер[животные![кошки]] ) И 0=[курит[Rothmans] животные[кошки]] И (^номер[курит[Rothmans]]+1=^номер[напиток[вода]] ИЛИ ^номер[курит[Rothmans]]-1=^номер[напиток[вода]] ) И 0=[курит[Rothmans] напиток[вода]] И (^номер[национальность[норвежец]]+1=^номер[цвет[синий]] ИЛИ ^номер[национальность[норвежец]]-1=^номер[цвет[синий]] ) И 0=[национальность[норвежец] цвет[синий]]
Ответ:
Ответ к данной задаче представлен в виде таблиц. Первая представляет собой связь между номером дома и национальностью жильца, т.е. в первом доме живет норвежец, во втором – датчанин и т.д. (Рисунок 4).
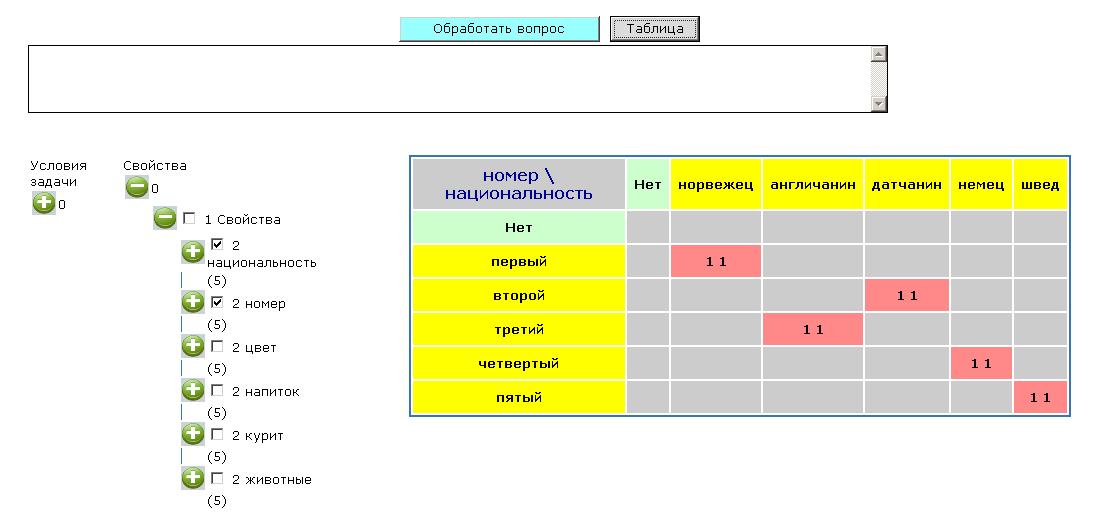
Рисунок 4. К задаче 4. Номер дома и национальность
В дереве свойств можно задать любую пару свойств для получения результата в виде таблицы. Так как собственно вопрос касался рыбок, то достаточно задать пару свойств "номер" и "животные". Результат показан на рисунке 5.

Рисунок 5. К задаче 4. Номер дома и животное
Задача 5.
Условие задачи:
По обвинению в ограблении перед судом предстали Иванов, Петров, Сидоров. Следствием установлено следующее:
1) Если Иванов не виновен или Петров виновен, то Сидоров виновен.
2) Если Иванов не виновен, то Сидоров не виновен.
Вопрос:
Виновен ли Иванов?
iФормирование входных данных:/i
(НЕ ([Фамилия![Иванов] Виновен]=0 ИЛИ [Фамилия[Петров] Виновен]=1) ИЛИ [Фамилия[Сидоров] Виновен]=1) И (НЕ ([Фамилия [Иванов] Виновен]=0) ИЛИ [Фамилия[Сидоров] Виновен]=0) И *Фамилия([*Фамилия]=1)
Ответ:
Ответ можно представить в виде таблицы, показанной на рисунке 6.
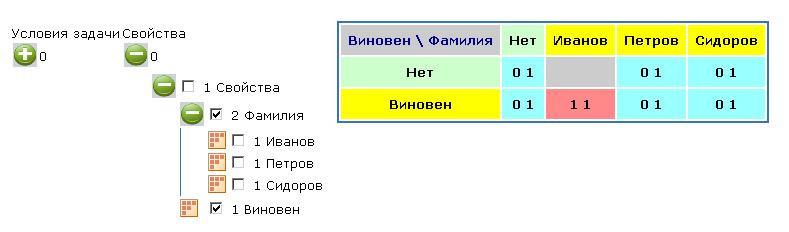
Рисунок 6. К задаче 5. Ответ в виде таблицы
Из таблицы видно, что Иванов виновен. Относительно же виновности Петрова и Сидорова сказать ничего нельзя. Если же в условия задачи добавыить еще одно условие, заключающееся в том, что виновным может быть только олин человек или никто (" И [Виновен]
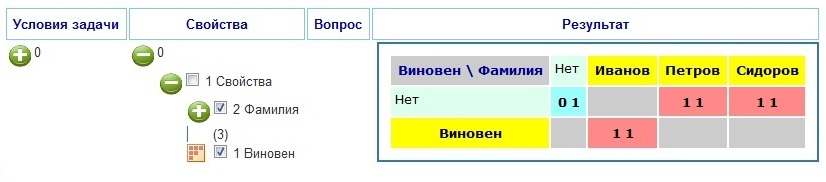
Рисунок 7. К задаче 5. Ответ в виде таблицы
Задача 6.
Условие задачи:
Это известная японская головоломка судоку, показанная на картинке (рисунок 8).
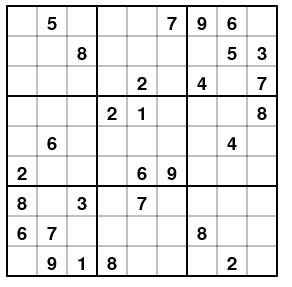
Рисунок 8. К задаче 6. Условия задачи
Вопрос:
Какие цифры расставлены в других клетках?
Формирование входных данных:
В этой задаче есть дополнительные улсловия, общие для всех судоку: в каждом столбце и в каждой строке, а также в каждом из 9 квадратов 3х3, каждая цифра встречается по одному разу. Входные данные, относящиеся к конкретной задаче, составляют небольшую часть всех данных. Сформированные входные данные размеещны на сайте, где также можно изменить для любой другой головоломки судоку и провести расчет.
Ответ:
Ответ дается в виде нескольких таблиц. Только на этих таблицах столбцы и ряды поменяны местами. На рисунке 9 показано расположение числа 1, на рисунке 10 – числа 2.
Таким образом можно выяснить расположение и других чисел.
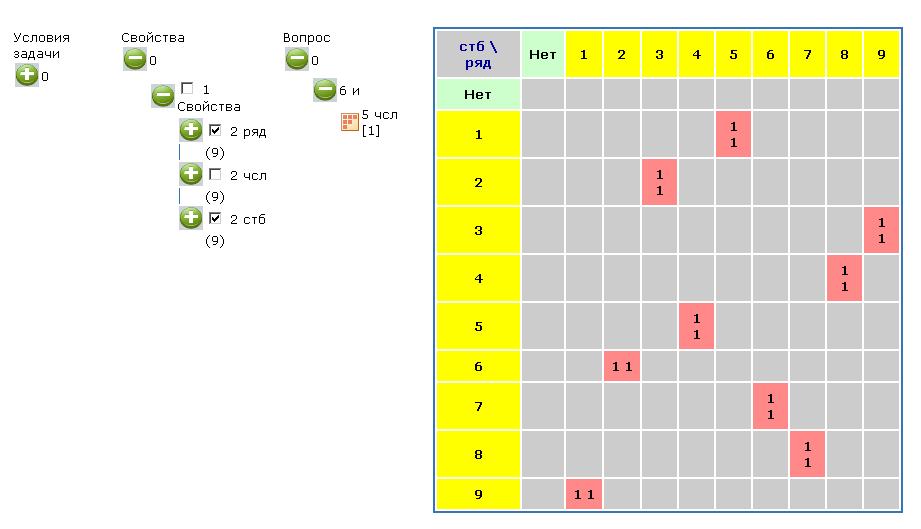
Рисунок 9. К задаче 6. Расположение числа 1
 Вам помочь или не мешать?
Вам помочь или не мешать?



