Главная

ПРОГРАММА НАХОЖДЕНИЯ РЕШЕНИЙ НЕКОТОРЫХ ЛОГИЧЕСКИХ ЗАДАЧ

Данная программа – это попытка запрограммировать правила логических выводов, описанные в книге Льюиса Кэрролла "Символическая логика". В этой программе решение задач ищется не с помощью дедуктивных рассуждений и логических выводов, а лишь в семантическом смысле: при наличии предпосылок, считающихся истинными, выясняется истинно или ложно некоторое утверждение.

При наличии набора условий некоторой ситуации обязательного "вывода" как такового из этих условий, или предпосылок, не существует. Из этих условий выводы можно делать любые – лишь бы они не противоречили условиям задачи. То есть, на любой поставленный вопрос можно получить ответ, согласующийся с заданными условиями задачи.

Исходим из того, что основа человеческого мышления – это слово, а язык – это средство логического мышления. Без языка (слов, словосочетаний и предложений) не возможен процесс рассуждений и логических выводов, т. е. то, что с каждым словом ассоциируется некий предмет, понятие, действие, признак, совершенно не влияет на соотношение между ними. Качество слов (их смысл) также не влияет на качество логических связей между ними.

Что касается образного (не выражаемого словами) мышления, которое присуще не только людям, то его трудно осознать, проследить и зафиксировать. Возможно, у человека образное мышление более сложное, чем у животных, но по сути не сильно отличается: оно представляет собой поиск в своей памяти аналогий, выяснение последствий найденной аналогии с последующим выводом похожих результатов из имеющейся ситуации. Приблизительно, как в пропорции: мы знаем, что 6 в три раза больше, чем 2. Имеем ситуацию в виде двух чисел 12 и 4. Замечаем аналогию: 12 и 6 соотносятся так же, как 4 и 2. Отсюда можем сделать вывод, что 12 в три раза больше, чем 4. Это, конечно, примитивный пример, так как образное мышление может включать в себя и другие, более сложные соотношения: вложенность, симметрию, перспективу, предельный переход и т.д. Все это очень трудно алгоритмизировать.

При анализе словесных рассуждений предполагается, что используемые в рассуждениях понятия "истина" и "ложь" – это свойство какой-либо фразы, составленной из слов. Все бессмысленные с точки зрения человека фразы можно считать ложными.

"Истина" и "ложь" рассматриваются в категориях "существует" или "не существует" какой-либо объект. Объектом назовем нечто, описываемое фразой (набором слов). Здесь использована теория системы координат: каждое слово – это отдельная координата, которая может принимать значения 0 или 1. Если в языке N слов, то количество различных фраз (объектов), без учета порядка слов (и падежей), будет равно 2^N.

В языке, однако, порядок слов часто имеет существенное значение. Например, имеются две фразы, состоящие из одинаковых (без учета падежей) слов, но описывающие разные состояния: "красный шар в синей коробке" и "синий шар в красной коробке".

В связи с этим структура координатного пространства была несколько усложнена: каждая координата-слово может принимать значения из множества: 0 плюс набор других слов. Кроме того, любое из значений, не равное 0, также может иметь значение, состоящее из 0 и набора других слов. Получается древовидная вложенность слов друг в друга.

Для наглядности введем обозначения: квадратными скобками обозначим значение координаты. В таком случае две вышеприведенные фразы будут записаны следующим образом: "шар[красный] в коробке[синей]" и "шар[синий] в коробке[красной]".

В случае, когда значение координаты может принимать значение всего лишь 0 или 1, то значение 1 опускается. Например, "шар в коробке[синей]". Вложенность значений может быть любой глубины, то есть, часть фразы может иметь следующий вид: "... в коробке[красной[ярко]] ...".

Следует отметить, что в такой системе координат даже если свойства обозначены одним словом, но имеют разных "родителей", то эти свойства считаются разными. Например, свойства "шар[красный]" и "коробка[красная]" - это разные свойства.

Конечно же, не любую фразу из языка можно разложить подобным образом. Но данная программа и не претендует на замену языка как средства общения. Здесь используется только одна его функция: средство передачи некоторой информации.

Так называемые фразы – это утверждения, которые, как было уже выше сказано, задают некоторый объект (или объекты) в координатном пространстве слов. Из теории координат следует, что, чем меньше условий накладывается на координаты (меньшее число уравнений), то тем больше размерность пространства, т. е. описываемого заданными уравнениями множества точек. Так как в нашем случае рассматриваются дискретные значения координат, то размерность вполне можно заменить словом размер, или мощность множества. Например, словом "автомобиль" описывается гораздо большее по количеству содержащихся в нем элементов множество, чем множество, которое описывается словами "легковой автомобиль". В вышеописанной терминологии эти две фразы можно записать как систему уравнений: "автомобиль = 1 и легковой = 1", т. е. объекты, описанные данной "системой уравнений", должны иметь свойства "автомобиль" и "легковой". Естественно, множество таких объектов имеет меньшую мощность, чем множество, описываемое уравнением "автомобиль = 1".

Ситуация "автомобиль = 1 и легковой = 1" запишется в виде "легковой[1] автомобиль[1]", или по условиям записи, когда выражение [1] должно быть опущено, запишется как "легковой автомобиль", что будет равнозначно записи "автомобиль легковой".

Ситуацию с легковыми автомобилями в другой системе координат можно также записать как уравнение "автомобиль = легковой", или в вышеприведенной форме: "автомобиль[легковой]".

В последующем знак равенства будет использоваться как можно меньше, так как он, по сути, является симметричным, что в данной работе не всегда приемлемо.

Знак равенства двух различных объектов имеет смысл лишь в случае, если эти объекты числа. Например, в геометрии равенство отрезков или углов подразумевает равенство их величин, выраженных числом. В данном же случае он использовался лишь по аналогии с системой уравнений "x=1, z=3".

Выше были описаны термины и способы задания множеств – условно и не всегда аналогично обще употребляемым значениям символов. В этой ситуации, так как разговор будет идти исключительно в терминах множеств и их мощностей, знаки следствия или равенства будут заменены знаком "подмножество". Кроме случаев задания количества элементов в множестве (его мощности): в этом случае знак равенства будет иметь свое математическое значение как равенство двух числовых величин.

Следует отметить, что для указания размеров множеств будут использоваться целые натуральные числа, ноль и знак М, задающий множество, аналогичное бесконечному по свойствам: размер объединения этого множества с любым другим тоже будет М (по аналогии с булевой алгеброй, где если А истинно, то А U В будет истинным для любого В).

Но это всего лишь аналог, так как указанное множество в любом случае будет конечным по количеству своих элементов: слова (координаты) будут описывать конкретные ситуации в пределах человеческого знания. А пока еще не известно, есть ли в природе (хотя бы в изучаемых пределах) такие элементы, которые составили бы счетное множество или, тем более, континуум.

Как и любая компьютерная программа, данная программа обрабатывает входные данные и выводит результат в виде выходных данных. Входные данные имеют структуру любой задачи – это описание некоторой ситуации (исходные данные) и формулировка вопроса, ответ на который должен быть на основе сложившейся ситуации. Разделение входных данных на две части дает возможность задавать вопросы по уже имеющейся ситуации, не описывая ее заново.

Следует отметить, что задача определения необходимой информации и постановки вопросов остается за человеком. Данная программа – это всего лишь средство для получения необходимой информации и к человеческим рассуждениям не имеет никакого отношения.

Часто правильная постановка вопроса и четкое понимание того, что же необходимо получить в качестве ответа – это почти готовое решение задачи.

Почти во всех логических задачах подтекстом идет очень много неявных условий, т. е. таких условий, о которых нужно просто догадаться – причем этого часто уже бывает достаточно, чтобы получить ответ.

В этой статье формированию условий задачи уделяется основное внимание.

Запись условий должна удовлетворять некоторым описанным ниже правилам – иначе программа при синтаксическом разборе этой записи может выдать сообщение об ошибке.

Как уже было выше сказано, для описания ситуации должны быть использованы слова. Так как программа "не знает" правил склонения и спряжения, то все одинаковые по значению слова должны быть и написаны одинаково. Строгое соответствие правилам лексики не обязательно - в силу того, что "слово" в данном случае всего лишь условное обозначение некоторого свойства объекта.

Язык и синтаксис предложений, задающих входные данные, содержит несколько специфических символов и слов, которые вследствие чего не могут быть использованы для описания свойств объектов. Это следующие слова и символы: "И", "ИЛИ", "НЕ", "(", ")", "[", "]", " ", ",", "*", "#", "^", ">", "<", "=", ">=", "<=", "!=", "не _", "+", "-".

Следует подчеркнуть, что слово не должно иметь внутри себя пробелов, а также запятых и вышеприведенных символов (кроме "И", "ИЛИ", "НЕ") и кавычек.

Стандартные логические связки (конъюнкция, дизъюнкция и отрицание) используются здесь на двух разных уровнях и, соответственно, обозначаются разными символами. На первом уровне - символами "И", "ИЛИ" и "НЕ", на втором уровне - пробелом, запятой и "не_".

Входные данные представляют собой строку элементов, соединенных друг с другом логическими связками "И", "ИЛИ", "НЕ" и скобками (первый уровень). То есть, иметь, например, такой вид: "А И (Б ИЛИ НЕ В)". Символами А, Б и В задаются множества и их размеры.

Правила задания множеств также связаны с логическими связками конъюнкции, дизъюнкции и отрицания, только в этом случае для их обозначения используются символы пробела, запятой и "не_" (второй уровень).

Выше был приведен пример с легковыми автомобилями и было показано, как одно свойство может быть вложено в другое. Комбинация всех свойств объектов как раз и будут задавать (определять) множество. Его размер задается с помощью квадратных скобок, в которые и заключается предложение, описывающее множество.

Легче это показать на примере. Есть условие задачи, состоящее в том, на ледовой дороге нет ни одного легкового автомобиля. Оно будет записано следующим образом:

Здесь пробелы между словами интерпретируются как конъюнкция. Если же необходимо задать условие, содержащее дизъюнкцию, то между словами или выражениями ставится запятая. Например, условие "В коробке лежат шары, которые могут быть синими или красными" задается следующим выражением:

Как уже было выше сказано, размер множества можно задать с помощью натуральных чисел, нуля и знаков "равно", "больше", "меньше", "больше или равно", "меньше или равно", "не равно". Наряду с натуральными числами и нулем в качестве размера множества используется символ М – как было сказано ранее, аналог размера (мощности) бесконечного множества, со следующим свойством: объединение множества, имеющего размер М, с любым другим множеством также имеет размер М. Равенство размера множества нулю задает пустое множество.

Кроме того, можно также задать с помощью перечисленных знаков равенства и неравенства соотношение между размерами двух множеств. Например, условие "синих шаров больше, чем красных" задается следующим образом:

Вышеописанные правила позволяют задать условия многих логических задач. В некоторых случаях условия задачи могут быть очень громоздкими, особенно когда имеется много неявных условий. В задаче про цветные шары неявно подразумевается, что каждый шар может быть только одного определенного цвета, т. е. объекта, обладающего свойствами "шар[красный синий]" не существует. Программа этого не знает, поэтому необходимо вводить дополнительное условие:

Если же цветов у шара может быть не два, а больше, то такие условия необходимо вводить для каждой пары цветов:

С целью избежать таких громоздких конструкций можно использовать некоторые правила.

Первое - это с учетом того, что задаются пустые множества (с мощностью равной 0), можно использовать запятые:

Такой вариант не намного упрощает запись. Есть еще один специальный способ записи, который относится к способу задания свойств и их значений: в конце свойства ставится восклицательный знак как символ единственности значения, которое может принимать данное свойство. Этот знак во всем предложении достаточно поставить один раз для свойства, - что и определит эту ее особенность. Например, в следующем выражении уже нет необходимости задавать специально равными пустому множеству все те множества, образуемые парами цветов шара:

Для облегчения записи условий задачи используются также символы, аналогичные кванторам существования и всеобщности в логике предикатов.

Любое предложение из логики предикатов может быть записано с помощью логики высказываний в том случае, когда область определения переменных является конечным множеством X. Предикатную константу P(x) в таком случае можно считать набором высказываний P₁=P(x₁), ... ,P_N=P(x_N), здесь N – количество элементов в множестве X. Формулу, использующую квантор всеобщности (∀xP(x)), можно записать в виде выражения P₁ ∧ ... ∧ P_N, а формулу, использующую квантор существования (∃ xP(x)), можно записать в виде P₁ ∨ ... ∨ P_N.

Примером рассуждения, не выразимого в логике высказываний, часто приводят следующий: "Все люди смертны. Сократ – человек. Следовательно, Сократ смертен".

Множество "всех людей" хоть и очень большое, но конечное. Поэтому можно ввести обозначения высказываний:

P_i – i-й человек, Q – смертен, S – Сократ.

В этих обозначениях вышеприведенное рассуждение записывается следующим образом:

(((P₁=>Q) ∧ ... ∧ (P_N=>Q)) ∧ ((S=>P₁) ∨ ... ∨ (S=>P_N)))=>(S=>Q)

В пределах задания одного множества нет необходимости использовать символы всеобщности или существования, так как существование или всеобщность какой-то переменной (слова) задается ее отсутствием:

• если мощность множества задается равной 0 (пустое множество), то отсутствие переменной означает, что пустым оно будет при ее любом значении;
• если же множество задается не пустым, то отсутствие переменной означает, что для некоторых ее значений (может быть, и всех, но не обязательно) множество будет не пустым.

В перечень значений переменной входит также и ее отрицание (равенство 0).

Необходимость использования кванторов возникает при задании условий, накладываемых на два или более множеств. Например, такое условие "гитарист и пианист учатся на одном факультете" можно представить как "существует факультет Ф, на котором они оба учатся", что запишется следующим образом:

[гитарист факультет[Ф]]=1 И [пианист факультет[Ф]]=1.

Если имеется перечень возможных факультетов (географический, филологический, исторический, ...), то это условие существования записывается как предыдущие выражения для каждого факультета, связанные друг с другом логической связкой "ИЛИ":

([гитарист факультет[географический]]=1 И [пианист факультет[географический]]=1 ИЛИ [гитарист факультет[филологический]]=1 И [пианист факультет[филологический]]=1 ИЛИ [гитарист факультет[исторический]]=1 И [пианист факультет[географический]]=1 ИЛИ ...)

Опять получается очень громоздкая запись. Для ее сокращения как раз и используется символ "#", задающий условие, аналогичное квантору существования. Предыдущее условие запишется следующим образом:

#факультет([гитарист #факультет]=1 И [пианист #факультет]=1)

Программа это выражение просто преобразует в предыдущее.

Квантор всеобщности в такой же интерпретации заменяется выражениями, связанными друг с другом логической связкой "И". Например, условие "имеется по одному шарику каждого цвета" запишется следующим образом:

([шар цвет[красный]]=1 И [шар цвет[синий]]=1 И [шар цвет[фиолетовый]]=1 И [шар цвет[белый]]=1 И ...)

Для упрощения записи можно использовать символ "*", задающий условие, аналогичное квантору всеобщности:

Программа, как и в предыдущем случае, заменит его более длинным выражением с использованием логической связки "И".

Что касается перечня значений свойства, то программа использует лишь те значения, которые встречаются во всей строке задания условия задачи. Так как во время синтаксического разбора строки кванторы обрабатываются в последнюю очередь, то это обеспечивает использование всех значений свойства, не зависимо от того, встретились они до или после квантора.

При задании множества по умолчанию подразумевается, что указывается размер задаваемого множества. Однако программа построена так, что вычислять можно любую функцию от задаваемого множества – лишь бы эту функцию можно было распознать при синтаксическом разборе.

В настоящий момент, помимо размера множества, реализована функция порядкового номера свойства в указанном множестве. Например, нужно указать, что "Вася пришел к финишу раньше Пети". Здесь свойство "место" имеет подузлы "место[первое]", "место[второе]" и т.д. – по количеству участников. Тогда вышеуказанное условие задается с помощью символа "^":

Единственное условие на задание порядка свойства: нумерация свойств будет производится в порядке их появления в предложении, т.е. чтобы свойство "место[первое]" имело порядковый номер меньше, чем свойство "место[второе]", нужно, чтобы первое появилось в предложении раньше второго.

При задании пустого множества "[свойство1,свойство2]=0" такая запись равнозначна записи "[свойство1]=0 И [свойство2]=0", т. е. задается условие, что не существует ни объектов, обладающих свойством "свойство1", ни объектов, обладающих свойством "свойство2".

При задании множества размера М "[свойство1,свойство2]=М" такая запись равнозначна записи "[свойство1]=М ИЛИ [свойство2]=М", т. е. задается условие, что объектов, обладающих свойством "свойство1" или обладающих свойством "свойство2", неограниченное количество.

Для преобразований из булевой формулы в форму, состоящую из записей первого и второго уровней, используется следующий порядок.

1. Булева формула F приводится к каноническому виду, т. е. раскрываются все скобки.
2. Канонический вид преобразуется в запись второго уровня D заменой дизъюнкции запятой, конъюнкции – пробелом, а знака отрицания – добавлением префикса "не_" к высказыванию.
3. Далее формула ¬F также приводится к каноническому виду.
4. Канонический вид формулы ¬F также преобразуется в запись второго уровня N.
5. Условия задачи, на основании принципа исключенного третьего, формулируются как "[D]=М И [N]=0".

При постановке вопроса, представляющего собой тоже булеву формулу V, истинность которой нужно узнать, необходимо для этой формулы получить аналогичным образом записи D и N, которые и ввести в качестве множеств для определения их размера.

• Формула V будет истинной, если D не пусто, а N пусто.
• Формула V будет ложной (т. е. 'НЕ V' – истинно), если D пусто, а N не пусто.
• В любом другом случае формула V при заданных условиях F не разрешима.

Следует отметить, что необходимость приведения булевой формулы к каноническому виду связана исключительно с техническими проблемами, так как на втором уровне нет "скобок", аналогичных обычным скобкам, используемым на первом уровне. То есть, запись "существуют легковые автомобили синие или черные" должна быть записана как "автомобиль[легковой (синий, черный)]>0", но поскольку на втором уровне нельзя использовать круглые скобки (недоработка программы), то это условие следует записать следующим образом: "автомобиль[легковой синий, легковой черный]>0", т. е. существуют автомобили легковые синие или существую автомобили легковые черные. Здесь "или" - обычное, т. е. согласно условию могут одновременно существовать и синие, и черные легковые автомобили.

Алгоритм решения задачи

Основа алгоритма решения задачи – это перебор всех возможных вариантов для нахождения нужного. Создаются соответствующие древовидные структуры условий задачи, позволяющие нужным образом осуществлять перебор вариантов, а также ускорять процедуру перебора. Все вычисления были отданы на откуп компьютеру на основании принципа: "Он железный – выдержит все".

Решение задачи производится в два этапа.

Первый этап – это моделирование ситуации, или этап исходных данных (условия задачи) без учета поставленного вопроса.

Синтаксический разбор условия задачи имеет целью определить количество и структуру свойств и множеств. Результатом являются два "дерева": дерево свойств (D_sv) и дерево условий задачи (D_us). Первое – это система координат, а второе – это система уравнений.

Для сокращения записи введем обозначения:

Элементарные множества получаются пересечением каждого из N_mn первичных множеств со всеми остальными первичными множествами. Число N_razb не превышает 2^N_mn. Кроме того, так как задача рассматривается в дискретной системе координат, то количество элементарных множеств не может превышать количество точек пространства, задаваемого этой системой координат, т.е. N_razb ≤ 2^N_mn ≤ 2^N_sv.

Нахождение разбиений производится путем обхода всех точек и проверки их на принадлежность первичным множествам. Ускорение этого этапа происходит за счет исключения из проверки точек, принадлежащих пустым множествам и так называемым отрицательным множествам, определяемым в процессе вычислений.

Система уравнений имеет следующий размер: количество строк – это количество первичных множеств (N_mn), количество переменных – это количество элементарных множеств (N_razb).

Система уравнений в стандартном виде – это набор уравнений и неравенств, накладывающих условия на значения переменных и связанных логической связкой "И". Если каждое уравнение записать в виде f_i(x₁, ... ,x_k)=0, то система уравнений запишется в виде

В стандартной форме это выглядит так:

	f1(x1, ... ,xk)=0
	...
	fm(x1, ... ,xk)=0

В данной работе рассматривается более широкое понятие системы уравнений и неравенств, когда используется не только связка "И", но также и "ИЛИ". Например, система уравнений и неравенств может иметь такой вид:

Порядок выполнения операций "И" и "ИЛИ" при подстановке определенных значений переменных x₁, ... ,x_k в уравнения соответствует общепринятому: при отсутствии скобок приоритетной является операция "И". Кроме того, условие "=0" может быть заменено условиями «>0», "<0", а также ">=0", "<=0", "!=0". Вместо 0 может использоваться любое число, а также другая функция.

Условиями задачи являются задания множеств и их размеров (или порядкового номера свойства), а также логические связи между ними. Уравнение на задание размера множества (или порядкового номера свойства) можно записать в следующем виде: "Размер(МНОЖЕСТВО_i)=P_i" (или "^свойство(МНОЖЕСТВО_i)=P_i"). Всего будет N_mn таких уравнений, причем знак равенства, как уже было сказано выше, может быть заменен для некоторых i знаками "больше", "меньше", "больше или равно", "меньше или равно", "не равно", а вместо P_i может быть "Размер(МНОЖЕСТВО_j)" (или "^свойство(МНОЖЕСТВО_j)"). Эти уравнения должны быть связаны друг с другом различными комбинациями "И" и "ИЛИ", а также скобок.

Следует отметить, что в комплект к операциям "И" и "ИЛИ" обычно добавляется операция отрицания "НЕ". В данном случае ее применение к уравнениям или неравенствам является излишним, так как она вполне покрывается знаками "равно", "больше", "меньше", "больше или равно", "меньше или равно", "не равно". Для общей же записи системы уравнений отрицание "НЕ" используется: например, для использования его перед скобками. Впрочем, если отрицание будет поставлено и перед уравнением или неравенством, а не только перед скобками, то программа воспримет его правильно. То есть, запись "НЕ Размер(МНОЖЕСТВО_i)=0" будет означать, что размер множества i не равен 0, или что "МНОЖЕСТВО_i не пусто". Равносильные записи: "Размер(МНОЖЕСТВО_i)!=0", "Размер(МНОЖЕСТВО_i)>0".

Переменными (неизвестными) в данной системе уравнений будут размеры элементарных множеств. Их количество равно N_razb. С учетом того, что элементарные множества не пересекаются друг с другом, размер каждого первичного множества будет суммой размеров тех элементарных множеств, их которых оно состоит, то есть, является их объединением.

Каждое уравнение (или неравенство) в левой части будет иметь простой вид: это сумма некоторых переменных (в случае задания размера множества). Количество этих переменных может быть от 1 до N_razb. Если x_i – размер i-го элементарного множества, то уравнение (или неравенство) размера множества для k-го первичного множества (f_k) примет вид:

где a_k,j может принимать значения 0 или 1.

В случае задания порядкового номера свойства функция определяется в общем виде и ее значение вычисляется только на этапе расчета.

Система уравнений S будет представлять из себя композицию из всех уравнений (или неравенств) для k от 1 до N_mn и логических связок "И", "ИЛИ", а также скобок и знака отрицания "НЕ". Решением этой системы уравнений будет множество наборов значений переменных (x₁, ... ,x_Nrazb), при которых S будет истинна, причем x_i может принимать значение лишь из множества целых неотрицательных чисел.

Если решение системы уравнений не существует, то это будет означать, что заданные условия не совместимы, т. е. противоречивы. Если же решение существует, то введем обозначение X = {X_r=(x_r,1, ... ,x_r,Nrazb), r=1, ... ,N_resh} – набор значений переменных, при которых система $S$ является истинной. Здесь N_resh – количество решений системы уравнений. Получение множества решений системы уравнений, т. е. множества X = {X₁, ... ,X_Nresh}, - это и есть цель первого этапа программы, который выше был определен как этап исходных данных.

Реализация нахождения множества X тоже основана на переборе возможных значений переменных x₁, ... ,x_k. Ускорение процедуры перебора возможных значений происходит за счет выделения из системы уравнений стандартной части S_st, имеющей вид:

	f1(x1, ... ,xNrazb)=0
	...
	fm(x1, ... ,xNrazb)=0

Такое выделение стандартной части возможно лишь в случае, когда самым верхним узлом формирования условий задачи является узел "И" и когда среди его подузлов имеются первичные множества, у которых задан размер в виде равенства целому положительному числу. Именно из этих множеств формируется стандартная система уравнений, решение которой позволяет существенно снизить размерность пространства значений, на котором ищется решение общей системы уравнений S, где S = S_st И Sdop.

Решение системы уравнений S_st основано на том, что система имеет очень простой вид диофантовых уравнений: коэффициенты уравнения принимают значения 0 или 1, а правый столбец – целые положительные числа P_i. Кроме того, решение ищется лишь среди целых неотрицательных чисел, не превышающих максимума среди P_i (P_max). Дальнейший алгоритм можно назвать применением метода Гаусса к конкретной задаче. Путем перестановки строк и столбцов добиваемся того, чтобы в левом верхнем углу матрицы было как можно больше нулей и их количество от начала строки не возрастало в следующей строке. Тогда первые ненулевых коэффициенты при переменных определят так называемые фиксированные переменные, значения которых будут вычисляться, и эти переменные не будут участвовать в общем переборе значений.

Здесь следует отметить, что, несмотря на простоту задачи нахождения решений системы уравнений S путем перебора, этот самый "перебор" может занять очень большое время счета, так как в общем виде количество возможных вариантов значений переменных равно P_max^Nrazb, а N_razb ≤ 2^Nsv. Однако, как показывает применение этой программы к конкретным задачам, выделение в системе уравнений стандартной части существенно снижает количество возможных вариантов значений переменных, а соответственно, и время счета.

В то же время при отсутствии стандартной части в системе уравнений ни что не может спасти вычисления от экспоненциального роста количества переменных, их возможных значений и, соответственно, времени расчета задачи. Вполне возможна ситуация, когда кажущимся приемлемым и вполне воспринимаемым человеческим разумом количество входных данных может породить неподвластные даже современному компьютеру объемы вычислений. В таких случаях часто вспоминают об интуиции как единственном средстве "увидеть" ответ на задаваемый вопрос. Вполне возможно, что человеческий мозг, возможности которого далеко еще не изучены, каким-то образом "проводит расчеты" и выдает ответ, согласующийся с условиями задачи.

Второй этап задачи – это постановка вопроса и получение ответа. Следует исходить из того, что постановка вопроса – это описание множества, размер которого и хотелось бы выяснить. То есть, формулировка вопроса производится по тем же правилам, по которым производится описание множеств в исходных данных (запись второго уровня), только без использования специальных символов "!", "#" и "*". Обозначим это множество M_vopr.

На формирование множества M_vopr накладывается ограничение: формировать его нужно лишь из слов, содержащихся в условиях задачи. Ограничение это связано с тем, что слова задают координатное пространство. Например, если есть система уравнений, связывающих x и y, то попытка решить задачу о том, чему при таких условиях будет равно z, не имеет смысла. В программе задано, что если в вопросе встречается слово не из системы координат, то она (программа) выдаст ошибку формирования множества.

Ответ на вопрос, пусто или нет множество Mvopr, находится с помощью следующего алгоритма.

Сначала среди набора множеств E_i определяются те, которые полностью содержатся в множестве M_vopr. Этот набор множеств обозначается V_min. Минимальная сумма значений размеров этих множеств при всех значениях из множества X определяет минимальный размер, который может иметь множество M_vopr, и обозначается K_min. Если K_min>0, то это значит, что множество M_vopr не пусто, т. е. ответ на вопрос будет "да".

Следует отметить, что набор множеств V_min может отсутствовать. В этом случае K_min=0.

Далее среди набора множеств E_i определяются множества, объединение которых содержит в себе множество M_vopr, т. е. все элементарные множества, имеющие непустое пересечение с множеством M_vopr. Этот набор множеств обозначается V_max. (Доказательство того, что M_vopr содержится в V_max основано на том, что при определении элементарных множеств обход совершался по всему координатному пространству дерева свойств.) Максимальная сумма значений размеров этих множеств при всех значениях из множества X определяет максимальный размер, который может иметь множество M_vopr, и обозначается K_max. Если K_max=0, то это значит, что M_vopr – пустое множество, т.е. ответ на вопрос будет "нет".

В случае, когда K_min=0 и K_max>0 ничего определенного о размере множества M_vopr сказать нельзя. Это значит, что при заданных условиях множество M_vopr может быть и пустым и не пустым, что никак не зависит от условий задачи, т. е. при заданных условиях ответ на вопрос будет "неизвестно".

Ответ (за исключением "неизвестно") на любой вопрос (или разрешимость любого вопроса), т. е. определение пусто или нет любое множество, заданное в системе координат дерева свойств, происходит в случае, когда каждое элементарное множество – это точка пространства координат, а также имеется всего одно решение X₁=(x₁,x₂, ... ) системы S. Если же имеется несколько решений, т. е. размер множества X=(X₁,X₂, ...) больше 1, то разрешимость любого вопроса будет в случае, когда нулевые значения i-ая координата (x_r,i=0) будет иметь при всех r, т. е. для любого i значение координаты x_r,i будет либо нулевым при всех r, либо положительным при всех r (при наличии первого условия: каждое элементарное множество – это точка пространства координат).

Если разбиение на элементарные множества произошло таким образом, что некоторое элементарное множество E_i содержит в себе несколько различных точек координатного пространства и значение x_r,i хотя бы при одном r больше 0, то в этом случае достаточно задать вопрос (M_vopr) как собственное подмножество множества E_i и тогда для множества M_vopr будет отсутствовать V_min, и следовательно K_min=0. Набор V_max для M_vopr будет состоять из одного элементарного множества E_i, а так как при некотором r x_r,i>0, то K_max>0, и ответ будет "неизвестно".

Для более удобного получения ответа используется также графическое представление ответа на заданный вопрос. По сути, это ответ сразу на несколько вопросов, которые составляют из себя двумерную таблицу по распределению некоторых свойств. Ниже на конкретных примерах будет показано, в каком виде представляется ответ графически.

Здесь приведены примеры задач, которые были решены с помощью описываемой программы. Собственно, на этих (и многих других) задачах и производилась отладка программы. Многие блоки и алгоритмы были написаны как раз в связи с тем, что они понадобились для решения какой-то конкретной задачи.

Структура программы состоит из нескольких этапов и подпрограмм. Это позволяет добавлять новые блоки и изменять уже существующие в соответствии с появляющимися потребностями. Во многом это касается этапа синтаксического разбора входных данных, о котором пока ничего не было сказано.

Синтаксический разбор предложений условий задачи и вопроса происходит в виде вложенных независимых алгоритмов, которые только обмениваются друг с другом входными и выходными данными.

Сначала выделяется текст, заключенный между двумя скобками (или от начала предложения до первой встреченной скобки, а также от последней скобки до конца предложения). На этом уровне также определяется соответствие между правыми и левыми скобками. Далее полученный текст анализируется на наличие и расположение логических связок "И", "ИЛИ", "НЕ", а также выделяется текст, заключенный между ними. На следующем уровне анализируется текст на наличие арифметических знаков, связывающих правую и левую часть отношения: "равно", "больше", "меньше" и т.п., и производится разбивка на левую и правую часть уравнения или неравенства.

Ну и так далее по нисходящей происходит анализ каждого полученного на предыдущем уровне текста. На последнем этапе анализируется свойство: если его еще не существует в дереве свойств, то оно добавляется.

Программа разбора написана без учета имеющихся и известных алгоритмов синтаксического разбора логических предложений (например, разбор предложений, написанных на SQL). Возможно, существует оптимальный и более эффективный алгоритм для решения этой задачи (синтаксического разбора предложения), применение которого позволит ускорить в этой программе процесс расчета и нахождение ответа.

В настоящее время описанный алгоритм реализован на "JavaScript" (для браузера "Internet Explorer") и "PHP" и размещен на сайте http://hsv.dtn.ru. Приведенные ниже задачи (и многие другие) были тестовыми для этого сайта.

Задача 1.

Эта задача представляет собой закон транзитивности и предложена здесь лишь для демонстрации способа формирования входных условий для программы.

Условие задачи:

Из A следует B, из B следует C.

Вопрос:

Истинно ли высказывание "из A следует C"?

Формирование входных данных:

Импликация "из A следует B" равносильна записи "НЕ А ИЛИ В". Таким образом, условие задачи преобразуется в запись: "(НЕ А ИЛИ В) И (НЕ В ИЛИ С)", или "НЕ А И НЕ В ИЛИ НЕ А И С ИЛИ В И НЕ В ИЛИ В И C"

Запись D:

[А В, не_А С, В не_В, В С]

Запись N:

[А не_В, В не_С]

Формирование вопроса:

Определить истинность формулы "НЕ А ИЛИ С". Для этой формулы запись D: "[не_А, С]", запись N: "[А не_С]".

Ответ:

[не_А, С] – "да" (не пусто).

[А не_С] – "нет" (пусто).

Т. е. формула "НЕ А ИЛИ С" истинна.

Задача 2.

Условие задачи:

X,Y,Z – целые неотрицательные числа, и X<Y,Y<Z,Z=4.

Вопрос:

Какие значения принимает X?

Формирование входных данных:

Так как X,Y,Z – целые неотрицательные числа, то в качестве их значений используется размер множества, задающегося свойством – именем переменной.

([X]<[Y] И [Y]<[Z] И [Z]=4 И [X Y,X Z,Y Z]=0).

Формирование вопроса:

[X]

Ответ:

K_min=0 и K_max=2, т. е. X может принимать значения от 0 до 2.

Задача 3.

Условие задачи:

Четверо мальчиков со своими отцами катались на колесе обозрения по два человека: взрослый и мальчик. Ни один мальчик не катался со своим отцом. Алексей Иванович катался с Леней. Андрей катался с отцом Коли. Тима катался с отцом Андрея. Федор Степанович катался с сыном Виктора Павловича. Виктор Павлович катался с сыном Алексея Ивановича.

Вопрос:

С кем катался Григорий Александрович, а также и другие взрослые? И как зовут отца каждого мальчика?

Формирование входных данных:

Составить входные данные для задачи не намного легче, чем ее решить. Главное, определить структуру переменных. В данной задаче условия были сформированы следующим образом:

( 1=[имя![АИ] кат] И 1=[имя[АИ] сын] И
1=[имя[ФС] кат] И 1=[имя[ФС] сын] И
1=[имя[ВП] кат] И 1=[имя[ВП] сын] И
1=[имя[ГА] кат] И 1=[имя[ГА] сын] И
1=[дети![Андрей] кат] И 1=[дети[Андрей] сын] И
1=[дети[Тима] кат] И 1=[дети[Тима] сын] И
1=[дети[Коля] кат] И 1=[дети[Коля] сын] И
1=[дети[Леня] кат] И 1=[дети[Леня] сын] И
#имя(1=[дети[Андрей] кат #имя] И 1=[дети[Коля] сын #имя]) И
#имя(1=[дети[Тима] кат #имя] И 1=[дети[Андрей] сын #имя] ) И
#дети(1=[#дети кат имя[ФС]] И 1=[#дети сын имя[ВП]]) И
#дети(1=[#дети кат имя[ВП]] И 1=[#дети сын имя[АИ]]) И
0=[не_имя, не_дети, кат сын, не_кат не_сын, имя[АИ] кат дети[не_Леня], 
имя[не_АИ] кат дети[Леня]])

Ответ:

Ответ к этой задаче представлен в комбинированной форме. Сначала задается вопрос-множество, а потом с учетом ответа строится таблица.

Рисунок 1. К задаче 3. Кто с кем катался

Рисунок 2. К задаче 3. Кто чей отец

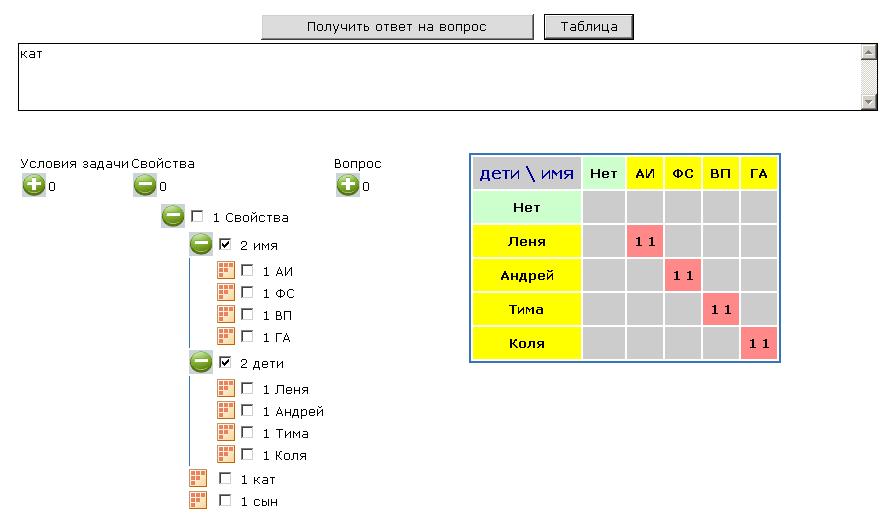
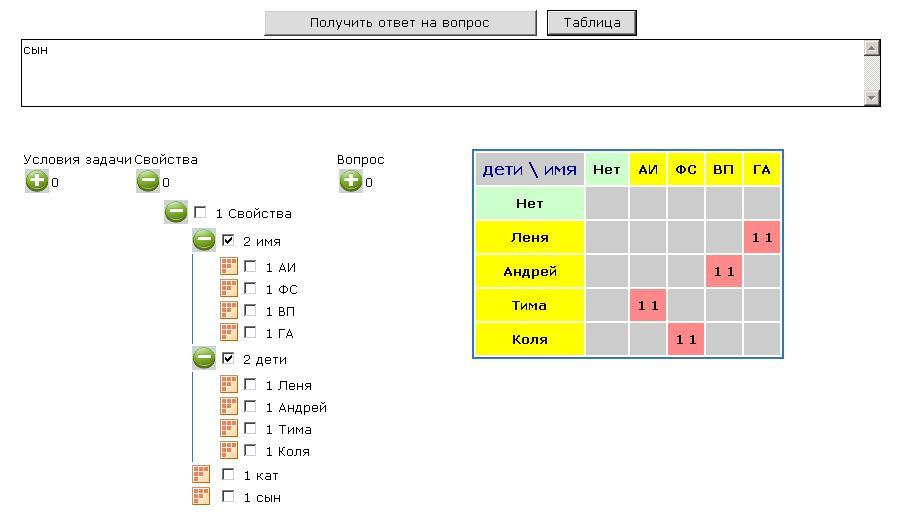
Если просто запросить ответ на вопрос "[сын]", то ответом будет – "множество имеет размер 4, т.е. не пусто" (Рисунок 3). Это следует напрямую из условий задачи: заданы 4 объекта, обладающие свойством "сын". Поэтому полезной будет информация, полученная в табличной форме.

Рисунок 3. К задаче 3. Ответ на вопрос

Задача 4.

Условие задачи:

Эта задача известна как задача Эйнштейна. Вот ее условие:
Есть 5 домов каждый разного цвета. В каждом доме живет по одному человеку отличной друг от друга национальности. Каждый жилец пьет только один определенный напиток, курит определенную марку сигарет и держит определенное животное. Никто из 5 человек не пьет одинаковые с другими напитки, не курит одинаковые сигареты и не держит одинаковое животное.\newline Кроме того:\newline Англичанин живет в красном доме, датчанин пьет чай, в желтом доме курят "Dunhill", норвежец живет в первом доме, немец курит "Marlboro", в среднем доме пьют молоко, курильщик "PallMall" держит птицу, швед держит собаку, в синем доме держат лошадь, курильщик "PhilipMoris" пьет пиво, в зеленом доме пьют кофе, зеленый дом находится слева от белого, курильщик "Rothmans" живет рядом с тем, кто держит кошку, норвежец живет около голубого дома, курильщик "Rothmans" живет рядом с тем, кто пьет воду.

Вопрос:

Кто держит рыбок?

Формирование входных данных:

Условия задачи сформулированы следующим образом:

[номер[первый]]=1 И [номер[второй]]=1 И [номер[третий]]=1 И 
[номер[четвертый]]=1 И [номер[пятый]]=1 И 
1=[национальность[англичанин] цвет![красный]] И 
1=[национальность[датчанин] напиток![чай]] И 
1=[цвет[желтый] курит![Dunhill]] И 
1=[национальность![норвежец] номер![первый]] И 
1=[национальность[немец] курит[Marlboro]] И 
1=[номер[третий] напиток![молоко]] И 
1=[курит[PallMall] животные![птицы]] И 
1=[национальность[швед] животные[собаки]] И 
1=[животные[лошади] цвет[синий]] И 
1=[курит[PhilipMoris] напиток[пиво]] И 
1=[цвет[зеленый] напиток[кофе]] И 
1=[животные[рыбы]] И 
0=[не_животные, не_напиток, не_курит, не_цвет, не_номер, 
не_национальность] И 
*животные([*животные]=1) И *напиток([*напиток]=1) И 
*курит([*курит]=1) И  *цвет([*цвет]=1) И 
*национальность([*национальность]=1) И 
^номер[цвет[зеленый]]+1=^номер[цвет[белый]] И
(^номер[курит[Rothmans]]+1=^номер[животные![кошки]] ИЛИ 
^номер[курит[Rothmans]]-1=^номер[животные![кошки]] ) И  
0=[курит[Rothmans] животные[кошки]] И
(^номер[курит[Rothmans]]+1=^номер[напиток[вода]] ИЛИ 
^номер[курит[Rothmans]]-1=^номер[напиток[вода]] ) И 
0=[курит[Rothmans] напиток[вода]] И
(^номер[национальность[норвежец]]+1=^номер[цвет[синий]] ИЛИ 
^номер[национальность[норвежец]]-1=^номер[цвет[синий]] ) И  
0=[национальность[норвежец] цвет[синий]]

Ответ:

Ответ к данной задаче представлен в виде таблиц. Первая представляет собой связь между номером дома и национальностью жильца, т.е. в первом доме живет норвежец, во втором – датчанин и т.д. (Рисунок 4).

Рисунок 4. К задаче 4. Номер дома и национальность

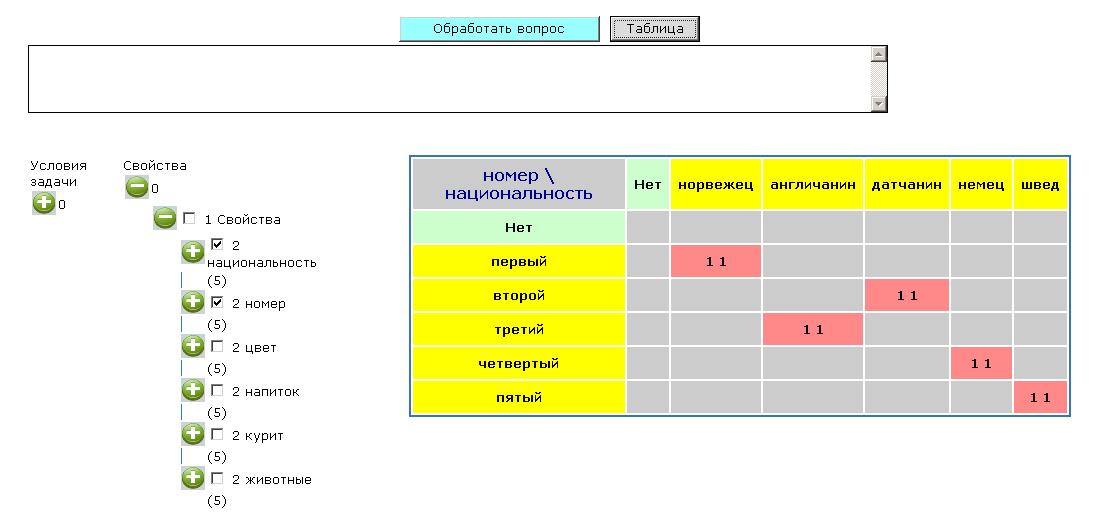
В дереве свойств можно задать любую пару свойств для получения результата в виде таблицы. Так как собственно вопрос касался рыбок, то достаточно задать пару свойств "номер" и "животные". Результат показан на рисунке 5.

Рисунок 5. К задаче 4. Номер дома и животное

Задача 5.

Условие задачи:

По обвинению в ограблении перед судом предстали Иванов, Петров, Сидоров. Следствием установлено следующее:
1) Если Иванов не виновен или Петров виновен, то Сидоров виновен.
2) Если Иванов не виновен, то Сидоров не виновен.

Вопрос:

Виновен ли Иванов?

Формирование входных данных:

(НЕ ([Фамилия![Иванов] Виновен]=0 ИЛИ 
[Фамилия[Петров] Виновен]=1) ИЛИ 
[Фамилия[Сидоров] Виновен]=1) И 
(НЕ ([Фамилия [Иванов] Виновен]=0) ИЛИ 
[Фамилия[Сидоров] Виновен]=0) И 
*Фамилия([*Фамилия]=1)

Ответ:

Ответ можно представить в виде таблицы, показанной на рисунке 6.

Рисунок 6. К задаче 5. Ответ в виде таблицы

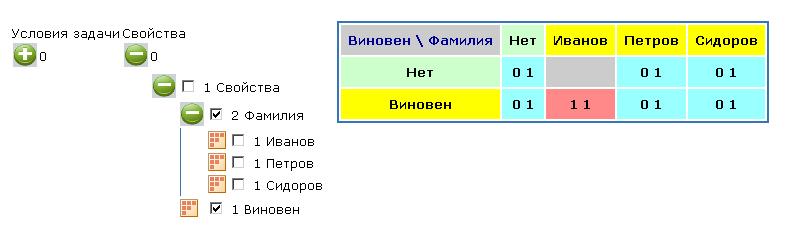
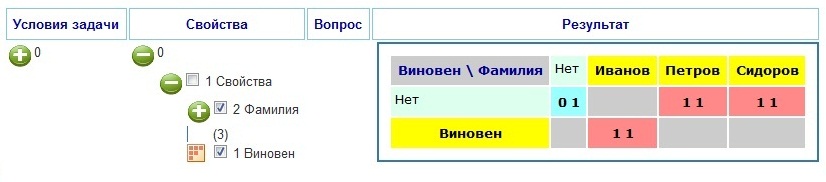
Из таблицы видно, что Иванов виновен. Относительно же виновности Петрова и Сидорова сказать ничего нельзя. Если же в условия задачи добавыить еще одно условие, заключающееся в том, что виновным может быть только олин человек или никто (" И [Виновен]<=1"), то рельтат будет следующим (Рисунок 7):

Рисунок 7. К задаче 5. Ответ в виде таблицы

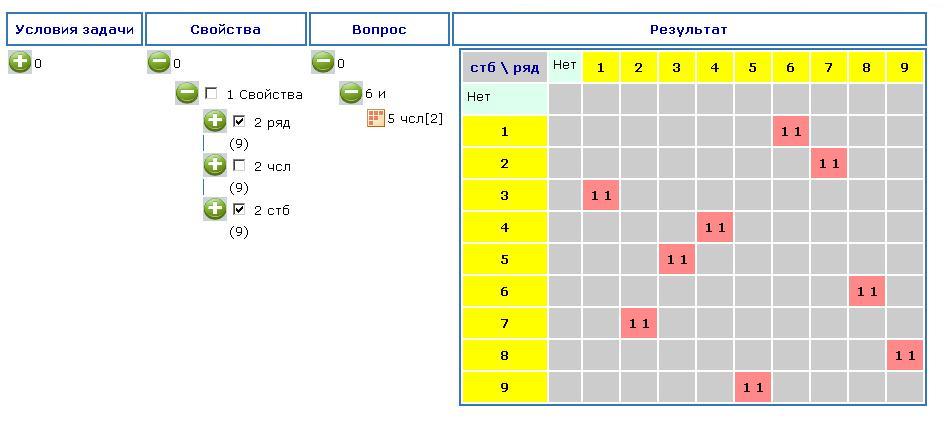
Задача 6.

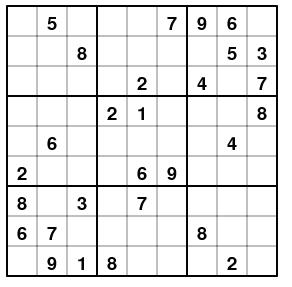
Условие задачи:

Это известная японская головоломка судоку, показанная на картинке (рисунок 8).

Рисунок 8. К задаче 6. Условия задачи

Вопрос:

Какие цифры расставлены в других клетках?

Формирование входных данных:

В этой задаче есть дополнительные улсловия, общие для всех судоку: в каждом столбце и в каждой строке, а также в каждом из 9 квадратов 3х3, каждая цифра встречается по одному разу. Входные данные, относящиеся к конкретной задаче, составляют небольшую часть всех данных. Сформированные входные данные размеещны на сайте, где также можно изменить для любой другой головоломки судоку и провести расчет.

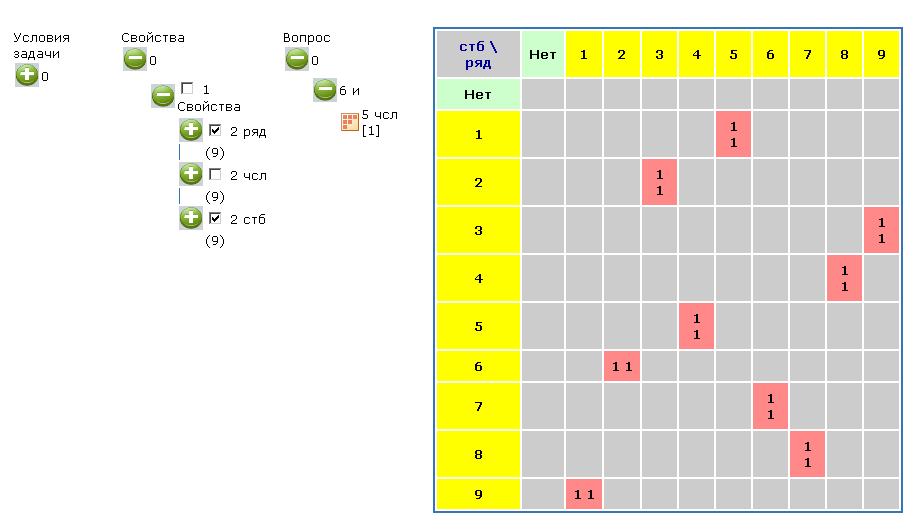
Ответ:

Ответ дается в виде нескольких таблиц. Только на этих таблицах столбцы и ряды поменяны местами. На рисунке 9 показано расположение числа 1, на рисунке 10 – числа 2.

Таким образом можно выяснить расположение и других чисел.

Рисунок 9. К задаче 6. Расположение числа 1

Рисунок 10. К задаче 6. Расположение числа 2

Приближенные вычисления

Если функция задана некоторой алгебраической формулой (например, f(x)=x+x²sinx), то приближенным значением функции в точке x₀ часто называется значение функции в некоторой, близкой к x₀, точке x₀+Δx, вычисление которого значительно проще, чем вычисление значения f(x₀)

Но в природе все обстоит наоборот. Например, положение свободного падающего тела в момент времени t рассчитывается по формуле s=-gt²/2, здесь s – расстояние в момент времени t от точки начала падения. Однако сама формула (не говоря уж о значении величины g), - это лишь приближенная (хоть и красивая) связь между временем и расстоянием, которое падающее тело проходит за это время. Поправка, получающаяся из формулы сложения скоростей в теории относительности, настолько мала, что никак не влияет на достоверность полученных результатов. Кроме того, и сама релятивистская формула – тоже, возможно, лишь приближенный вариант связи физических, реальных величин.

Математика – это лишь приближенная модель реального мира. Эффективность применения математических результатов в современной технике, физике и других областей естествознания позволяет надеяться (или, по крайней мере, мечтать), что с развитием, усовершенствованием и уточнением (на основе экспериментальных данных) формул математические модели будут все ближе и ближе приближаться по точности к реальному миру.

Надежды на это связаны с тем, что элементы математики встречаются в природе. Солнце, Луна и многие другие космические образования имеют форму шара (пусть и не геометрически точного), то есть математического объекта с определенными свойствами оптимальности как решения некоей математической задачи. Да и числа Фибоначчи тоже являются математическим объектом.

Польза математики заключается в том, что она может дать представление о той части реального мира, которая недоступна или нецелесообразна для исследований. Например, не стоит к падающему телу каждый раз привязывать рулетку и секундомер, чтобы получить необходимые данные о положении тела в определенный момент времени. (Хотя как раз именно в таких исследованиях и родилась идея формулы свободного падения).

Или еще пример – изучение так называемых элементарных частиц. Для прямого исследования их свойств у человека нет возможностей, так как человек с помощью своих чувств не может «заглянуть» в микромир. И сегодняшние результаты о частицах – это сплошная математика, для которой исходными данными являются всего лишь проявления взаимодействия этих частиц с макромиром, - а не сами они.

Люди также не могут протянуть рулетку от Земли до Луны или Солнца, чтобы измерить расстояние, но математические расчеты могут дать представление об этих расстояниях, пусть и приближенно, но с удовлетворительной для некоторых нужд степенью точности.

Впрочем, математика может помочь познавать реальный мир лишь при условии непрерывности пространства и времени (и других физических объектов и процессов): когда абстрагирование (предельный переход) дают значение в точке. Например, в известной притче о слепых мудрецах, исследующих слона по частям, применение математического метода интегрирования может дать, действительно, представление о слоне. Точность, конечно, зависит от «показаний» мудрецов, их достоверности и достаточности. Но при увеличении плотности «показаний» результат будет все больше и больше приближаться к слону. Но опять же лишь в случае предположения о непрерывности мира. Ведь, мы можем все больше и больше уточнять результат о «слоне», хотя в самой точке значением может быть «заяц». Кстати, в таком случае (существовании точек разрыва мира) Ахиллес может никогда не догнать черепаху.

Непрерывности природы и происходящих в ней процессов пока вопрос открытый.